Tetrads of the 1-3-5-7-9-11 Eikosany on a 37-key Synthesizer
Source:vignettes/articles/tetrads-on-37-key-synth.Rmd
tetrads-on-37-key-synth.RmdThe scale table
scale <- cps_scale_table(root_divisor = 33) # 1-3-5-7-9-11 Eikosany default
print(scale)
#> note_name ratio ratio_frac ratio_cents interval_cents degree
#> <char> <num> <charFrac> <num> <num> <num>
#> 1: 1x3x11 1.000000 1 0.00000 NA 0
#> 2: 3x5x9 1.022727 45/44 38.90577 38.90577 1
#> 3: 1x5x7 1.060606 35/33 101.86668 62.96090 2
#> 4: 3x9x11 1.125000 9/8 203.91000 102.04332 3
#> 5: 1x7x11 1.166667 7/6 266.87091 62.96090 4
#> 6: 5x7x9 1.193182 105/88 305.77668 38.90577 5
#> 7: 3x5x11 1.250000 5/4 386.31371 80.53704 6
#> 8: 1x3x7 1.272727 14/11 417.50796 31.19425 7
#> 9: 7x9x11 1.312500 21/16 470.78091 53.27294 8
#> 10: 1x5x9 1.363636 15/11 536.95077 66.16987 9
#> 11: 3x7x9 1.431818 63/44 621.41797 84.46719 10
#> 12: 5x7x11 1.458333 35/24 653.18462 31.76665 11
#> 13: 1x9x11 1.500000 3/2 701.95500 48.77038 12
#> 14: 3x5x7 1.590909 35/22 803.82168 101.86668 13
#> 15: 1x3x9 1.636364 18/11 852.59206 48.77038 14
#> 16: 1x5x11 1.666667 5/3 884.35871 31.76665 15
#> 17: 3x7x11 1.750000 7/4 968.82591 84.46719 16
#> 18: 1x3x5 1.818182 20/11 1034.99577 66.16987 17
#> 19: 5x9x11 1.875000 15/8 1088.26871 53.27294 18
#> 20: 1x7x9 1.909091 21/11 1119.46296 31.19425 19
#> 21: 1x3x11' 2.000000 2 1200.00000 80.53704 20
#> note_name ratio ratio_frac ratio_cents interval_cents degree
#> <char> <num> <charFrac> <num> <num> <num>The keyboard map
map <- keyboard_map(scale)
print(map)
#> Key: <note_number>
#> note_number name_12edo octave_12edo note_name ratio_frac degree
#> <num> <char> <num> <char> <char> <num>
#> 1: 0 C -1 1x3x11 1 0
#> 2: 1 C# -1 3x5x9 45/44 1
#> 3: 2 D -1 1x5x7 35/33 2
#> 4: 3 D# -1 3x9x11 9/8 3
#> 5: 4 E -1 1x7x11 7/6 4
#> ---
#> 124: 123 D# 9 3x9x11 9/8 3
#> 125: 124 E 9 1x7x11 7/6 4
#> 126: 125 F 9 5x7x9 105/88 5
#> 127: 126 F# 9 3x5x11 5/4 6
#> 128: 127 G 9 1x3x7 14/11 7
#> period_number freq cents ref_keyname ref_octave ref_offset
#> <num> <num> <num> <char> <num> <num>
#> 1: -3 32.70320 2400.000 C 2 0
#> 2: -3 33.44645 2438.906 C 2 39
#> 3: -3 34.68521 2501.867 C# 2 2
#> 4: -3 36.79110 2603.910 D 2 4
#> 5: -3 38.15373 2666.871 D# 2 -33
#> ---
#> 124: 3 2354.63009 9803.910 D 8 4
#> 125: 3 2441.83861 9866.871 D# 8 -33
#> 126: 3 2497.33494 9905.777 D# 8 6
#> 127: 3 2616.25565 9986.314 E 8 -14
#> 128: 3 2663.82394 10017.508 E 8 18The chord table
chords <- cps_chord_table(scale)
print(chords)
#> Key: <chord_index, is_subharm>
#> chord degrees chord_index is_subharm
#> <char> <char> <int> <num>
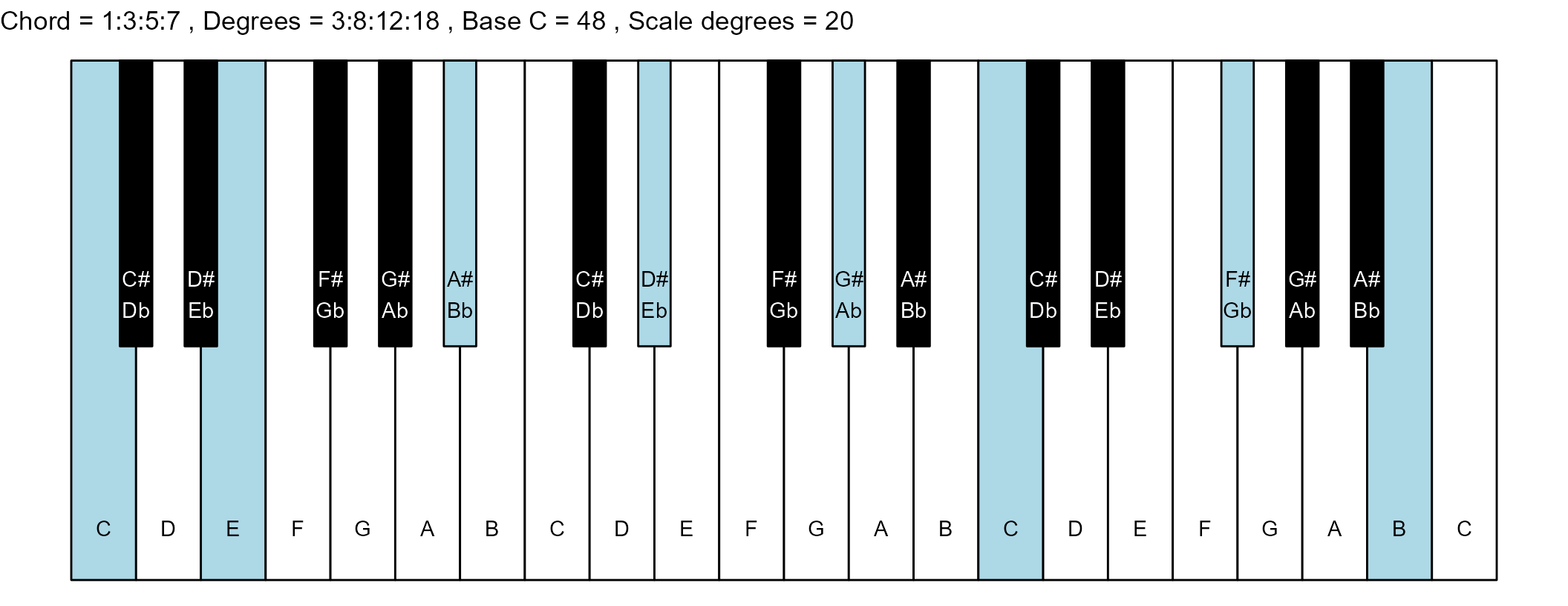
#> 1: 1:3:5:7 3:8:12:18 1 0
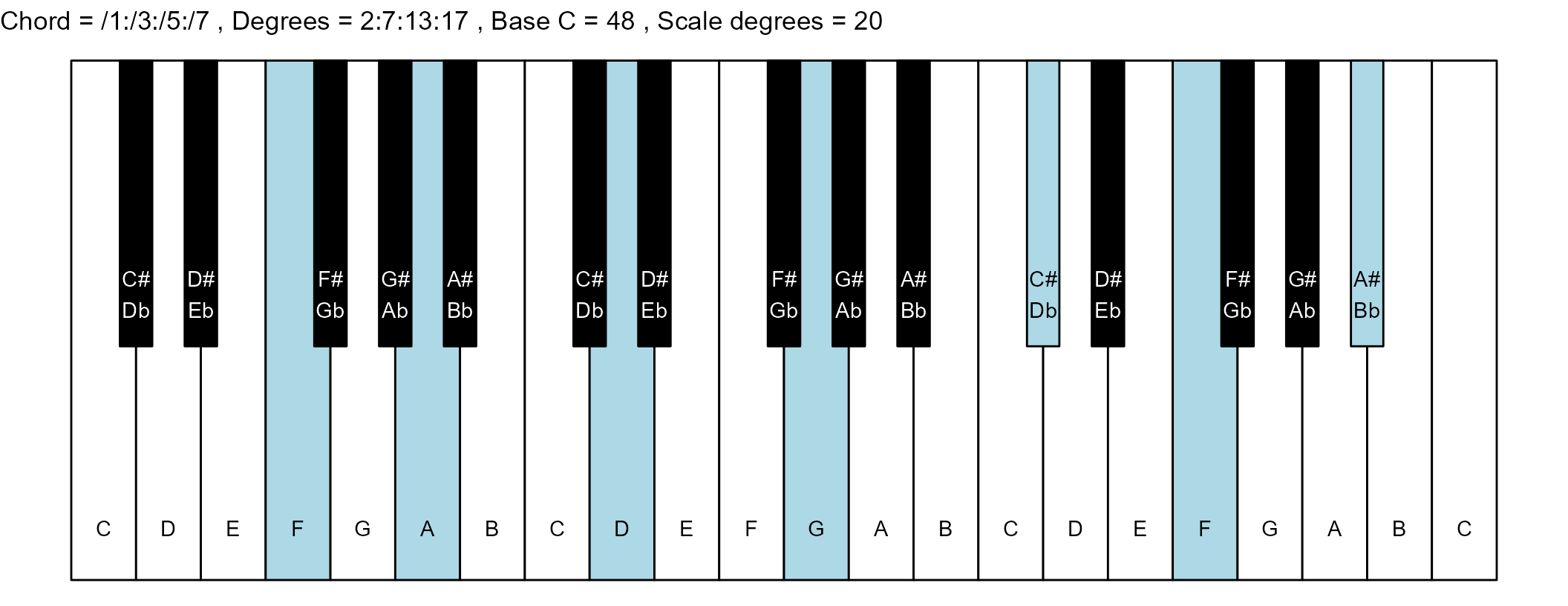
#> 2: /1:/3:/5:/7 2:7:13:17 1 1
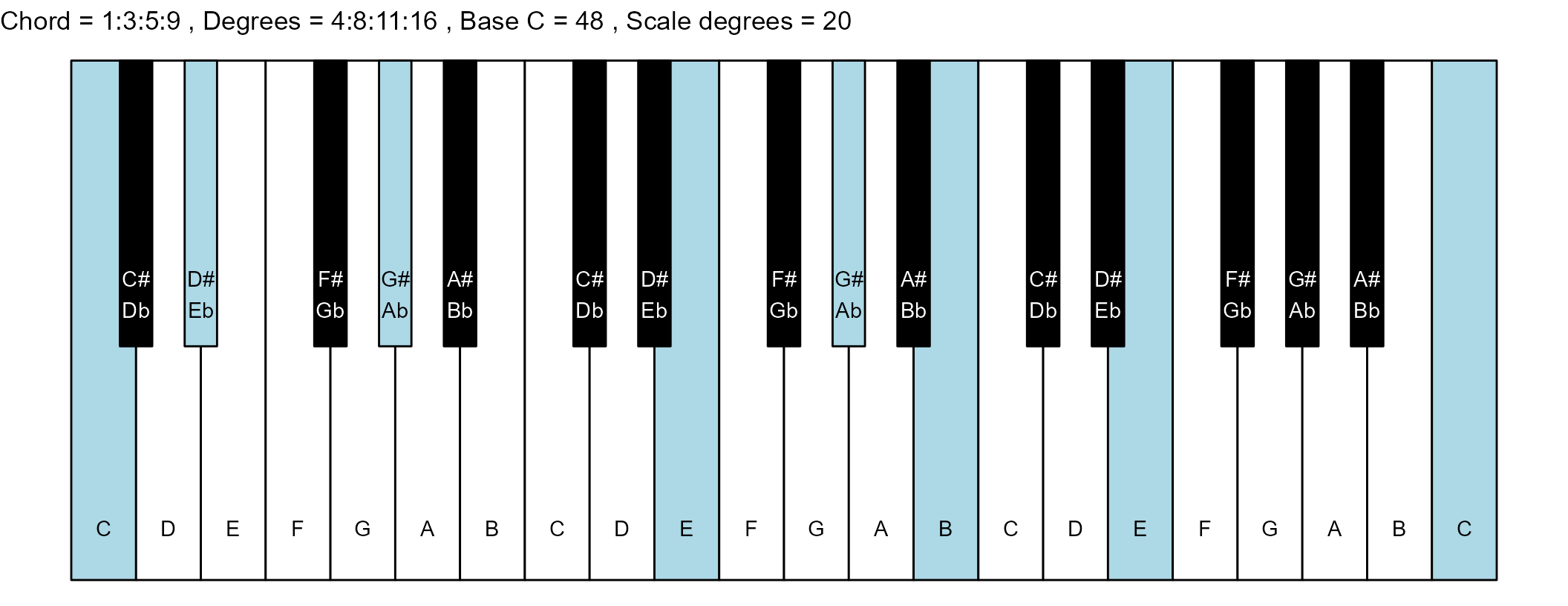
#> 3: 1:3:5:9 4:8:11:16 2 0
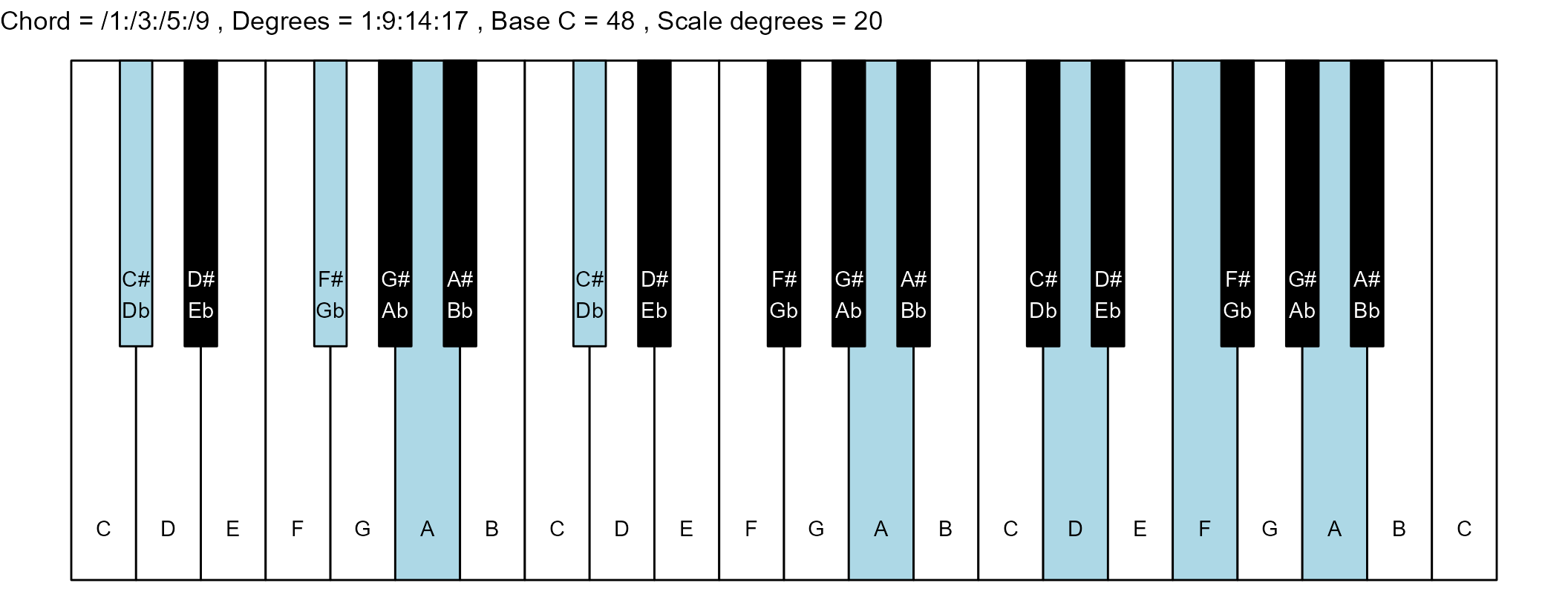
#> 4: /1:/3:/5:/9 1:9:14:17 2 1
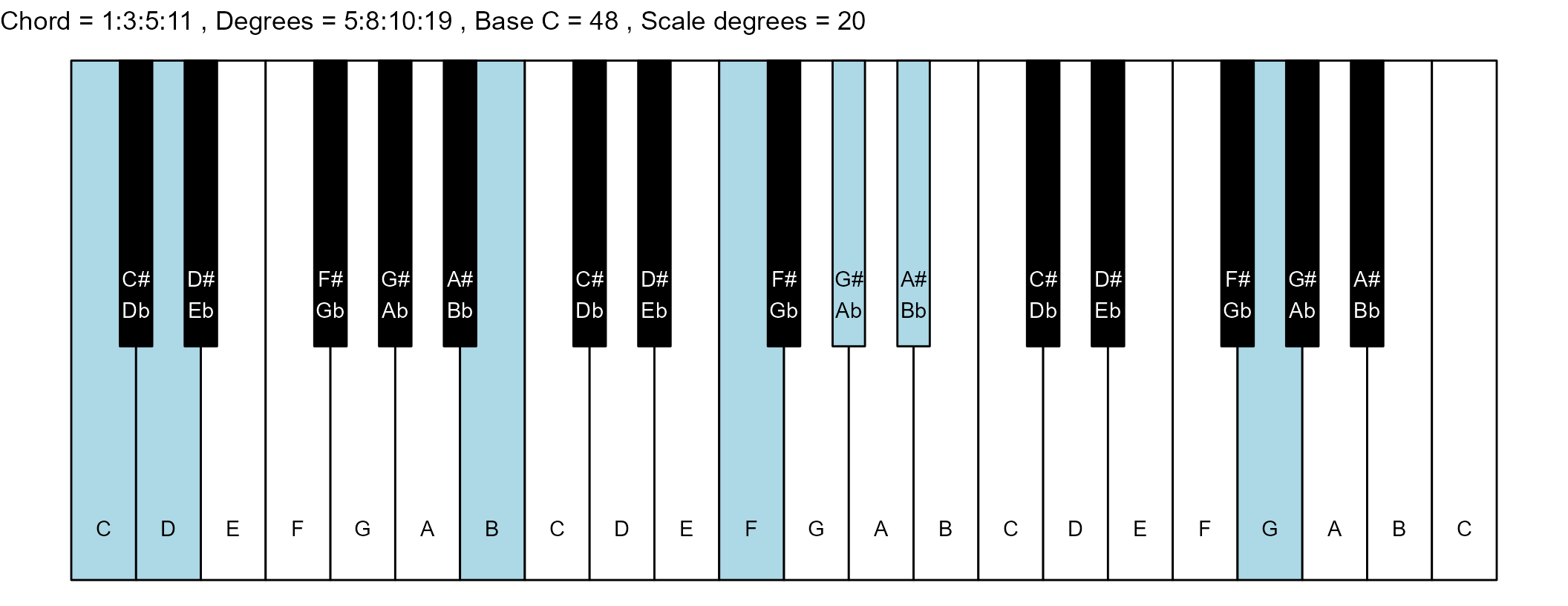
#> 5: 1:3:5:11 5:8:10:19 3 0
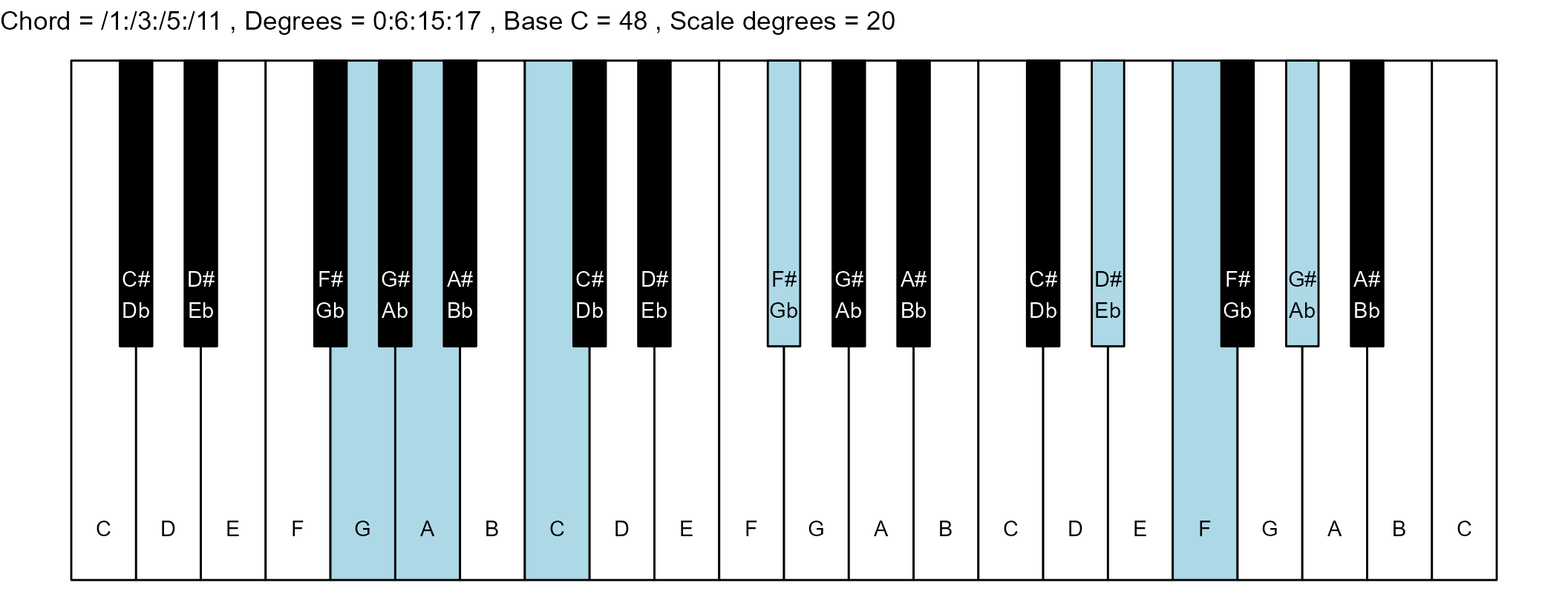
#> 6: /1:/3:/5:/11 0:6:15:17 3 1
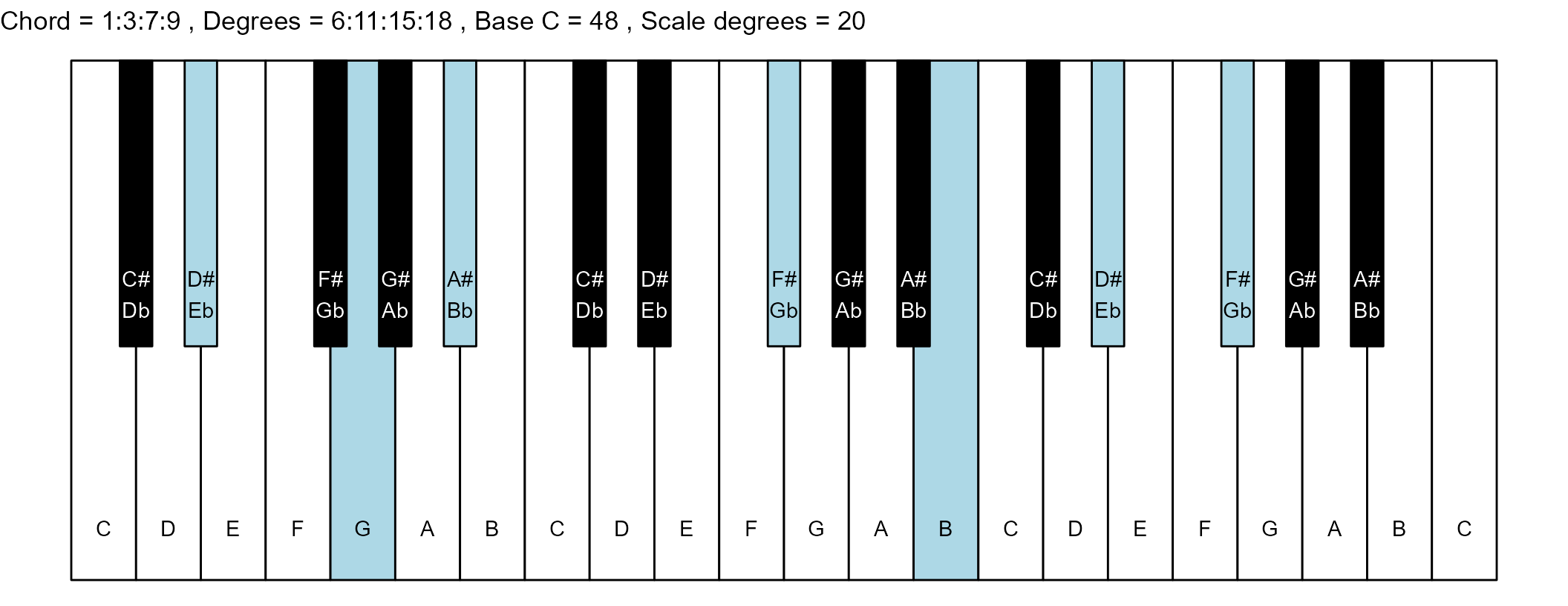
#> 7: 1:3:7:9 6:11:15:18 4 0
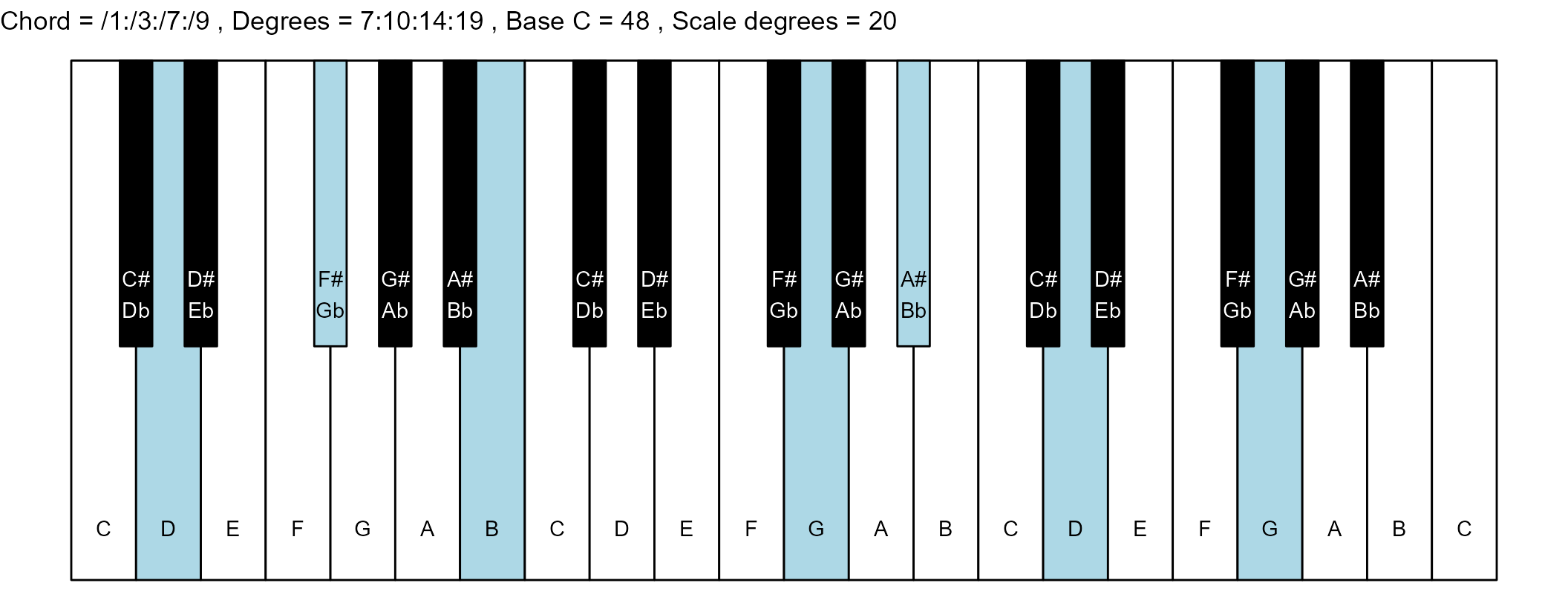
#> 8: /1:/3:/7:/9 7:10:14:19 4 1
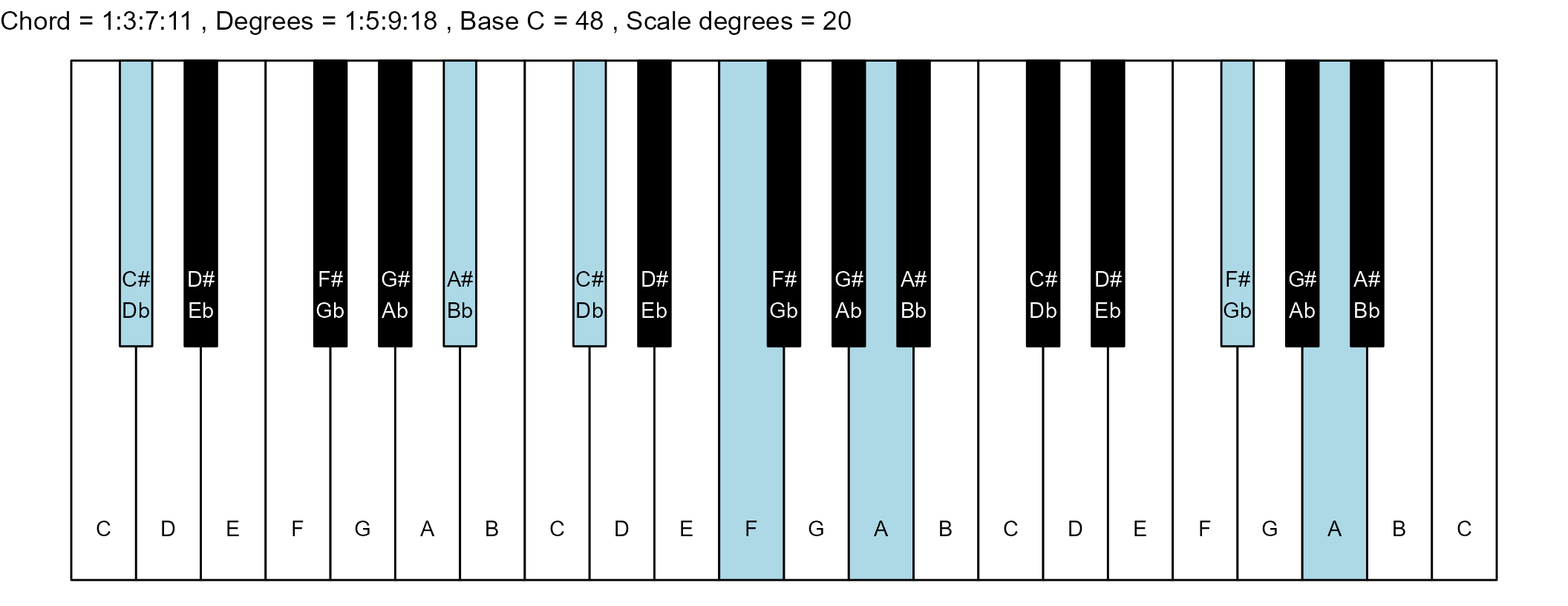
#> 9: 1:3:7:11 1:5:9:18 5 0
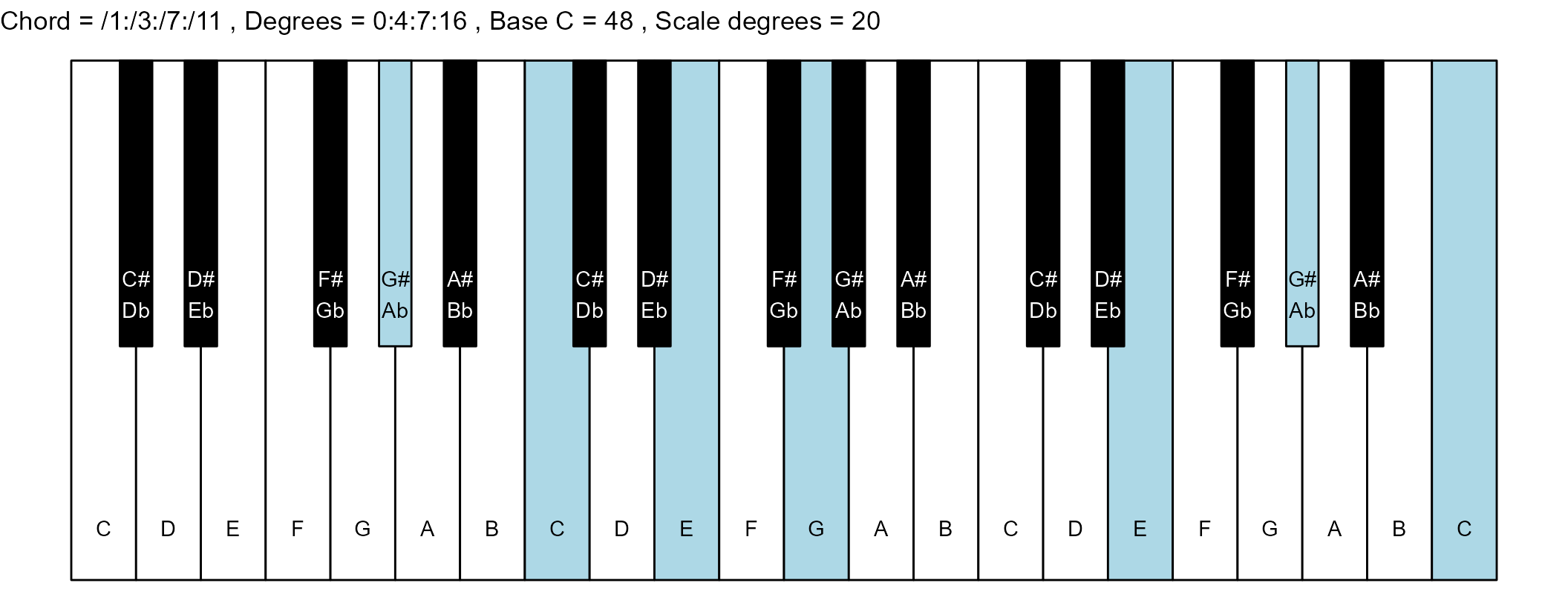
#> 10: /1:/3:/7:/11 0:4:7:16 5 1
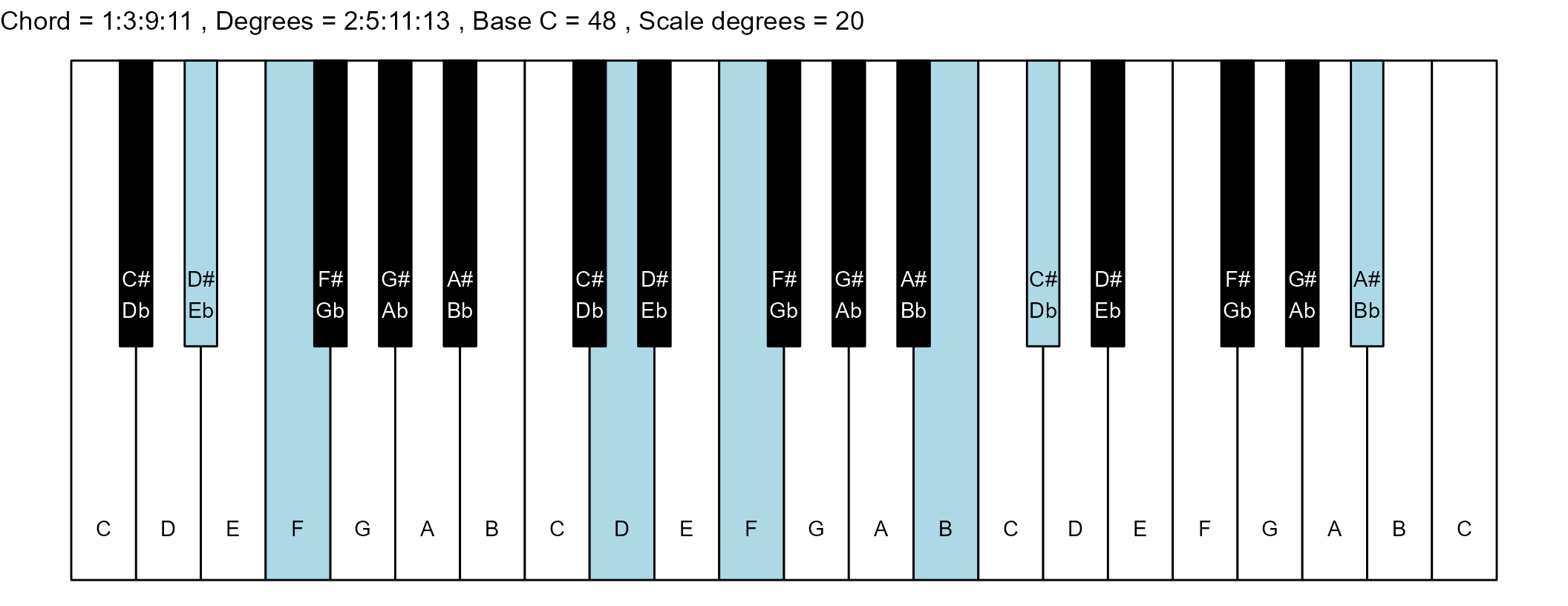
#> 11: 1:3:9:11 2:5:11:13 6 0
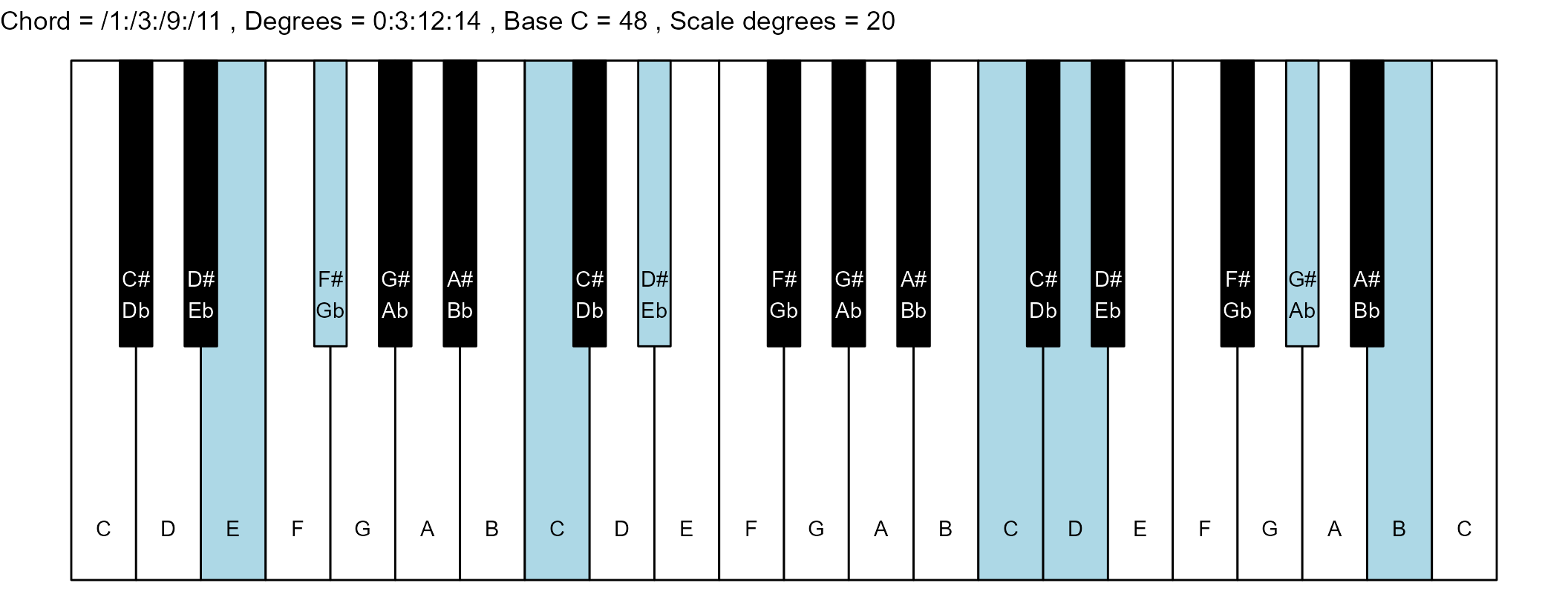
#> 12: /1:/3:/9:/11 0:3:12:14 6 1
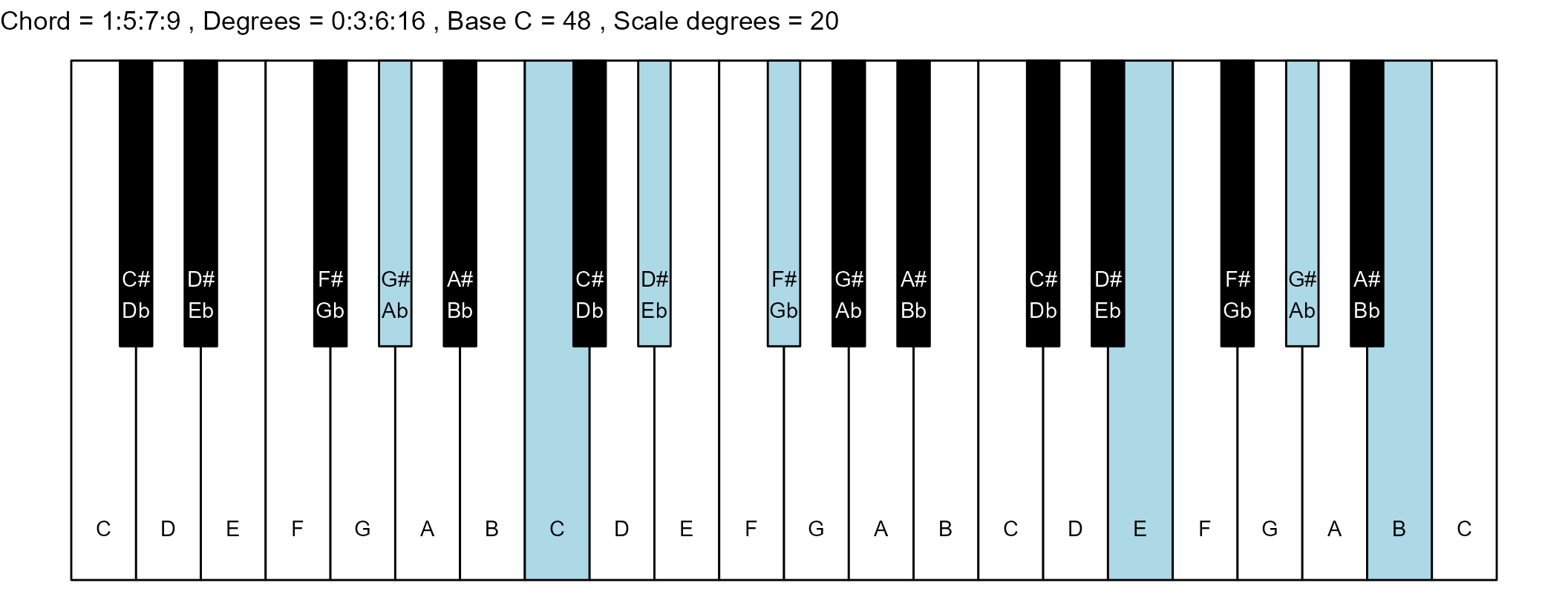
#> 13: 1:5:7:9 0:3:6:16 7 0
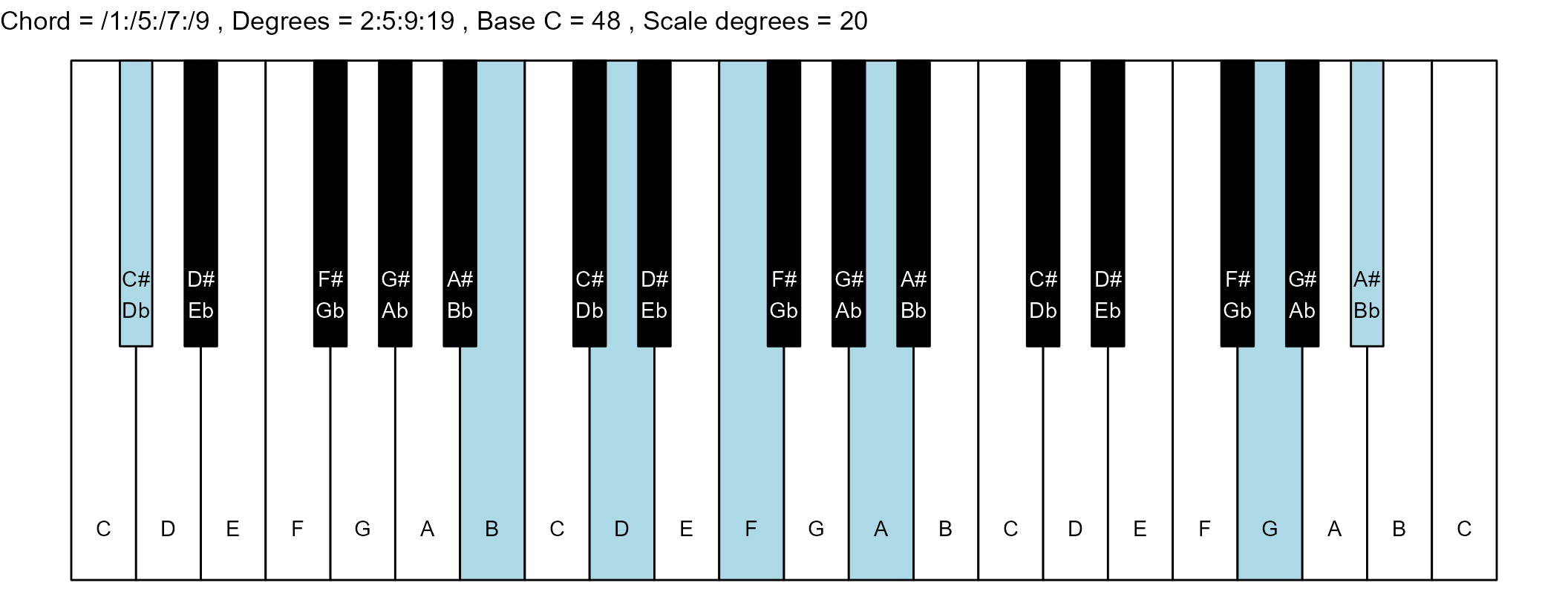
#> 14: /1:/5:/7:/9 2:5:9:19 7 1
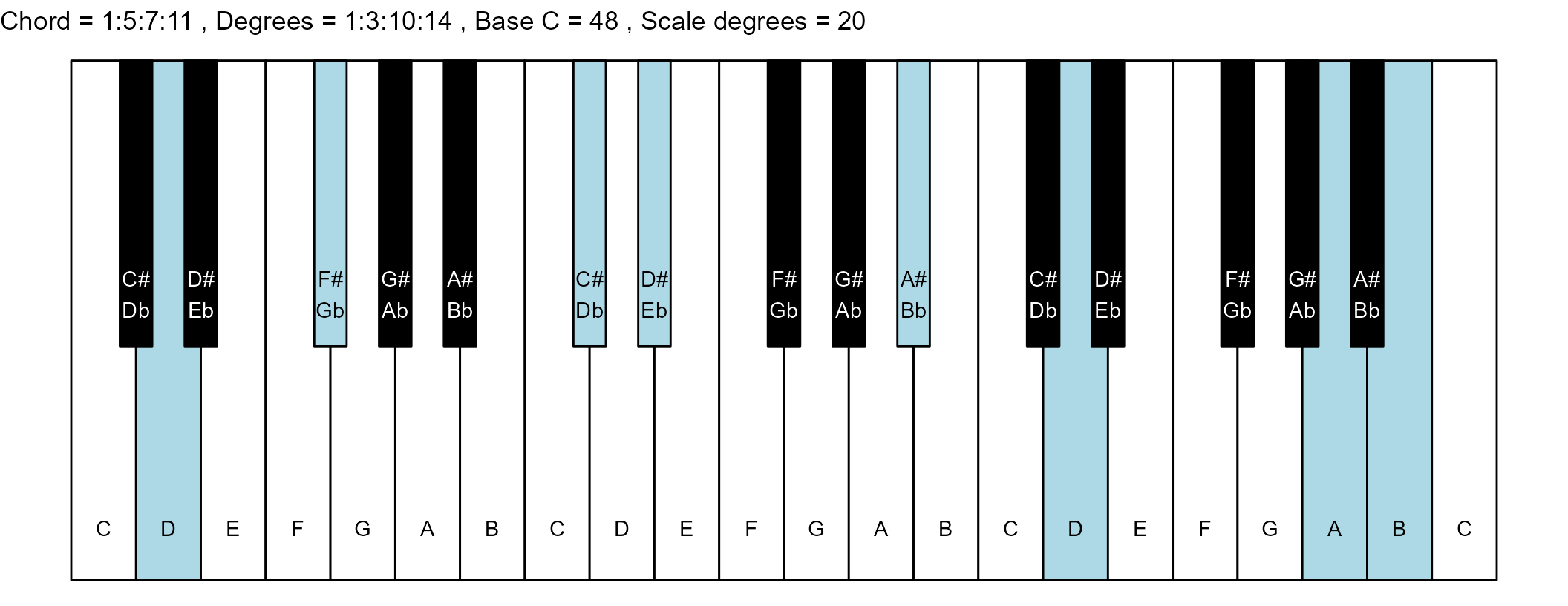
#> 15: 1:5:7:11 1:3:10:14 8 0
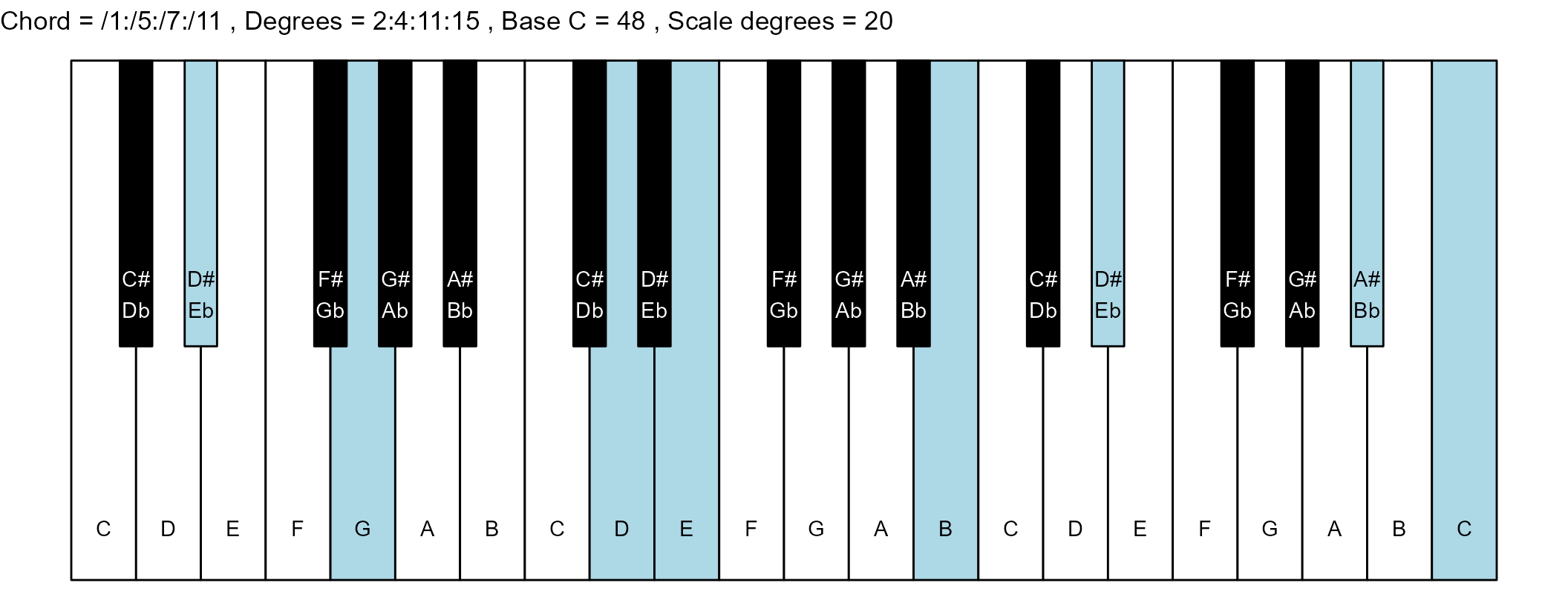
#> 16: /1:/5:/7:/11 2:4:11:15 8 1
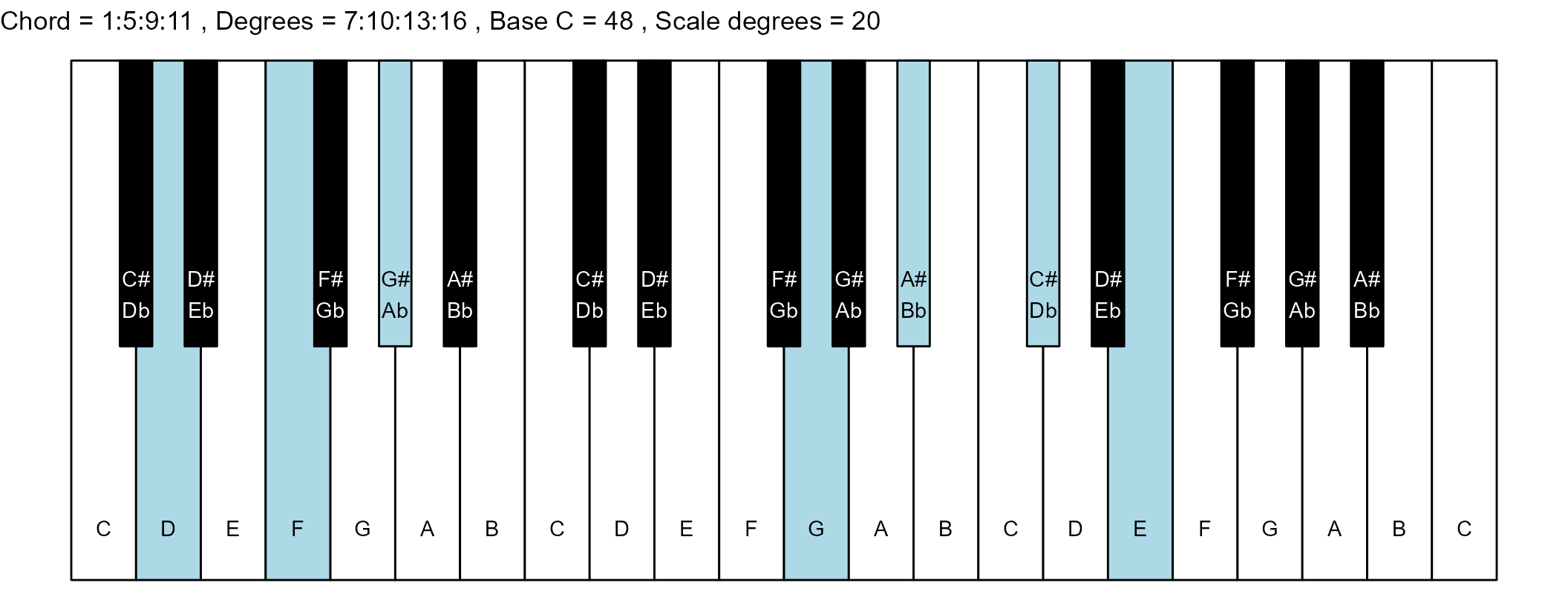
#> 17: 1:5:9:11 7:10:13:16 9 0
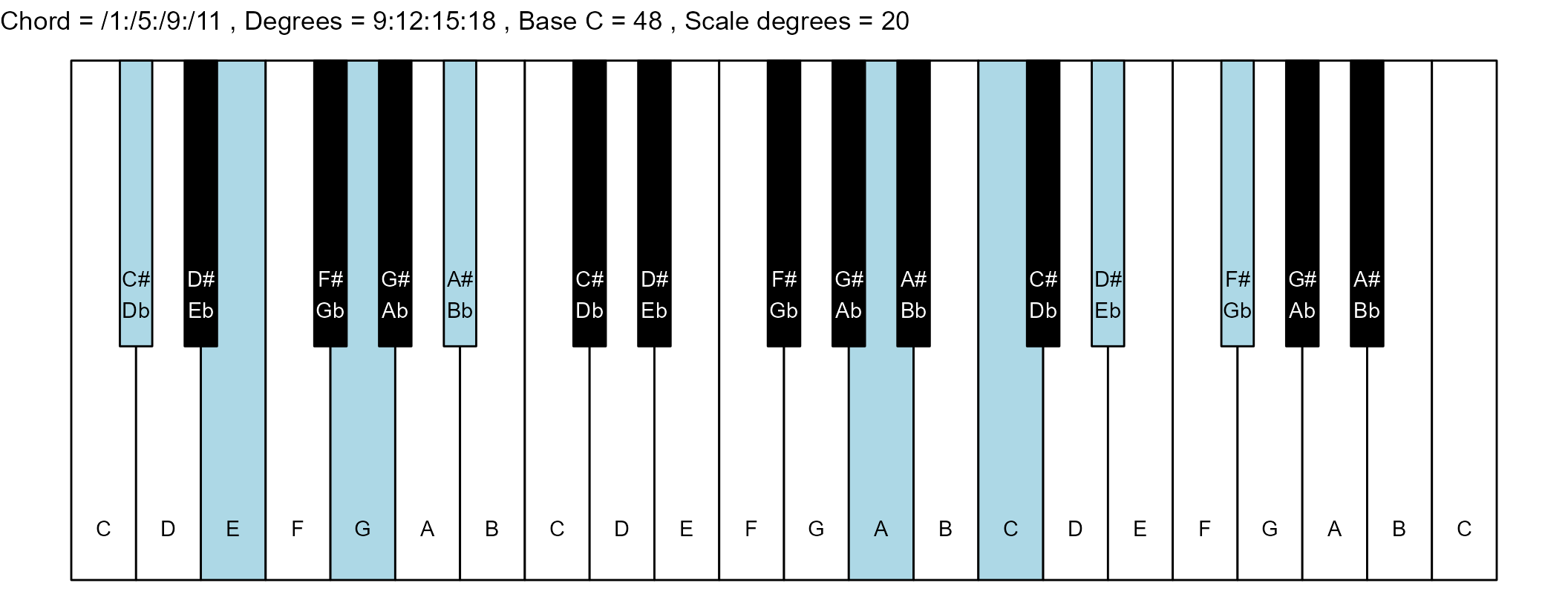
#> 18: /1:/5:/9:/11 9:12:15:18 9 1
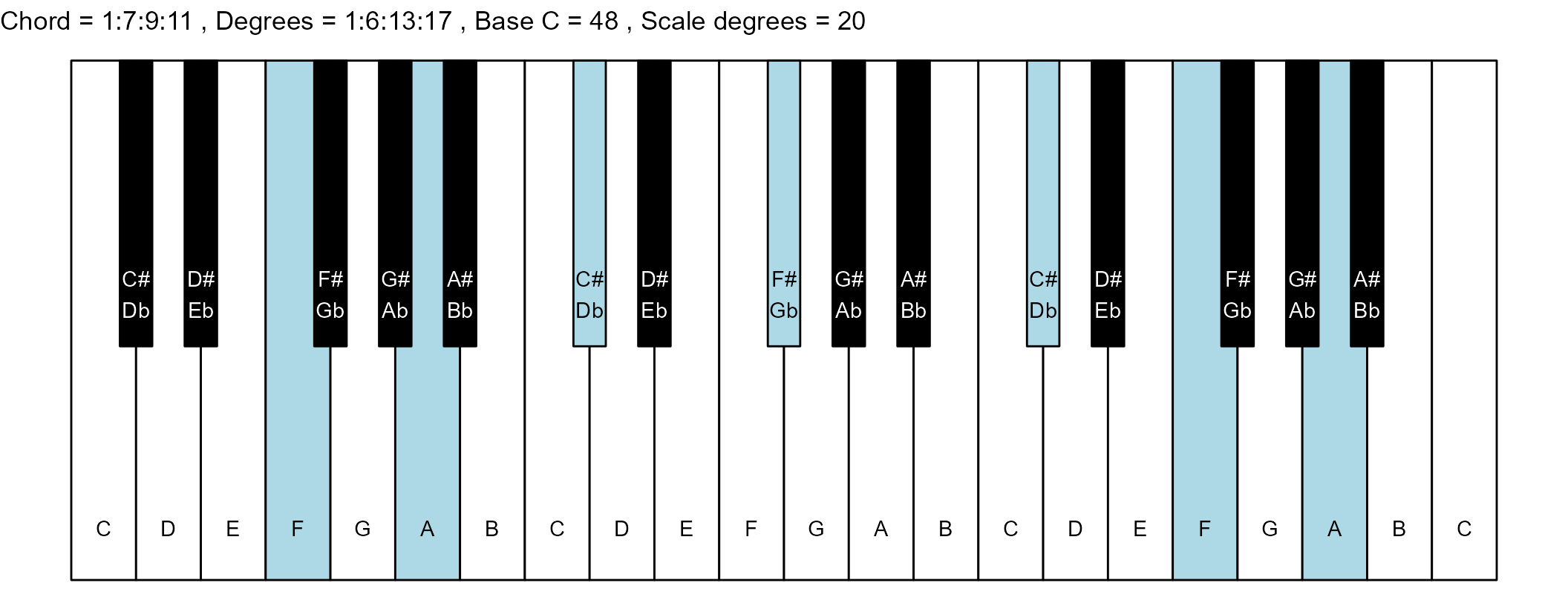
#> 19: 1:7:9:11 1:6:13:17 10 0
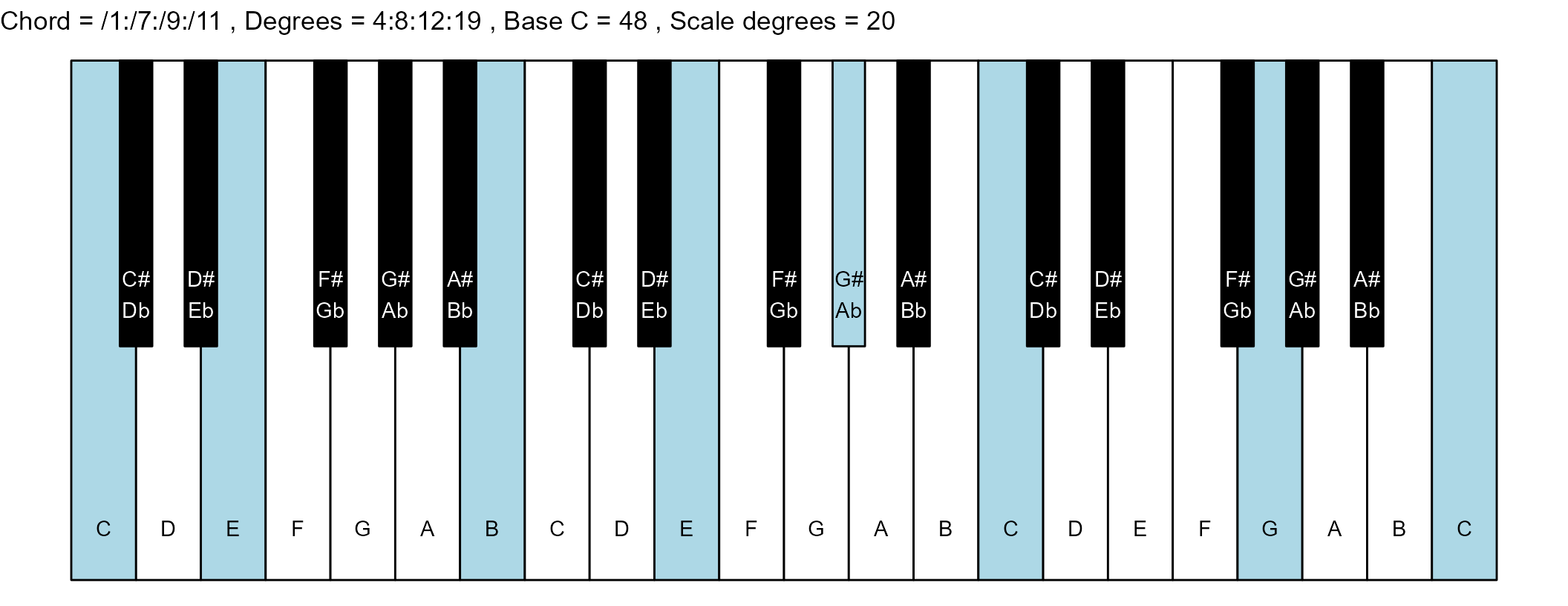
#> 20: /1:/7:/9:/11 4:8:12:19 10 1
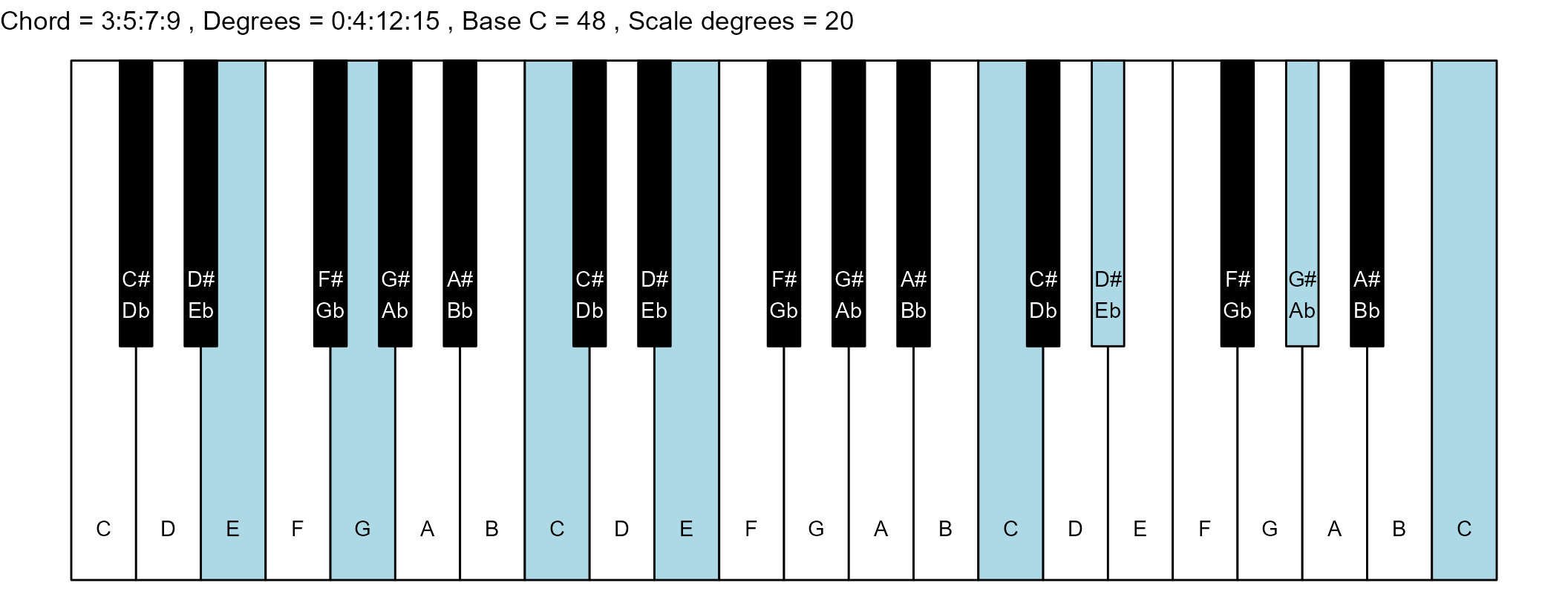
#> 21: 3:5:7:9 0:4:12:15 11 0
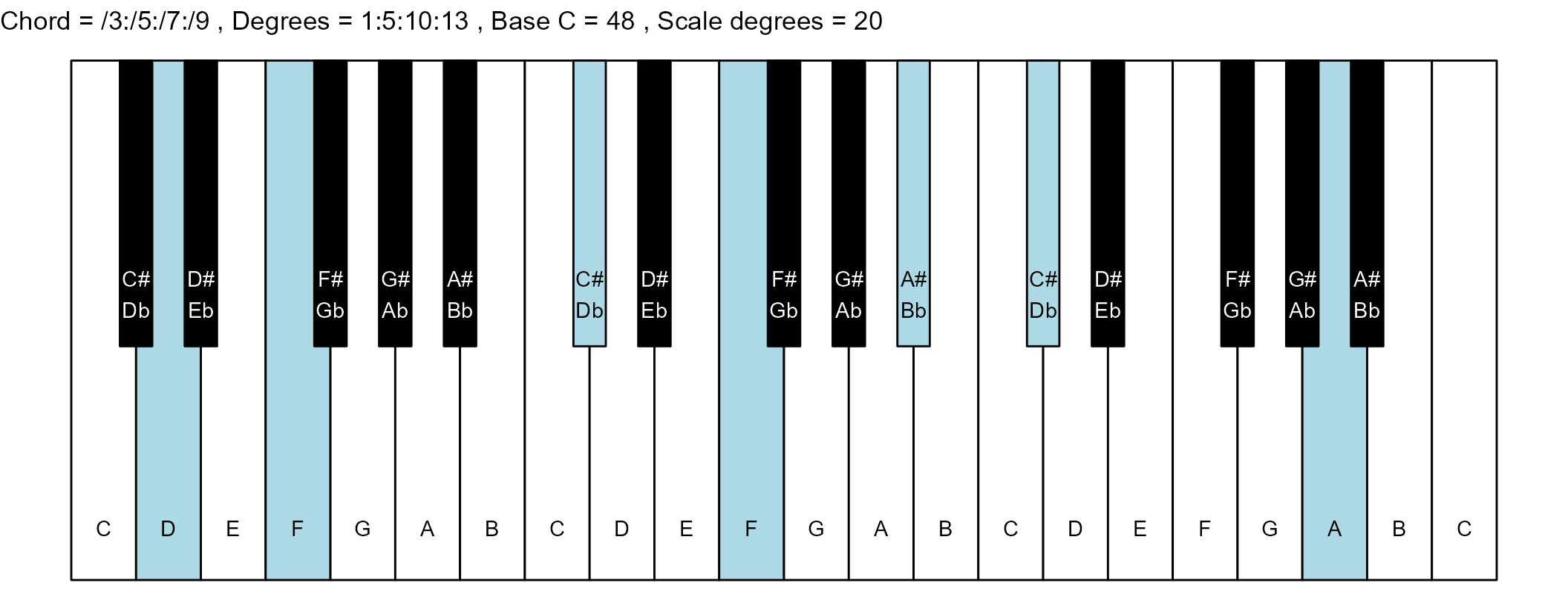
#> 22: /3:/5:/7:/9 1:5:10:13 11 1
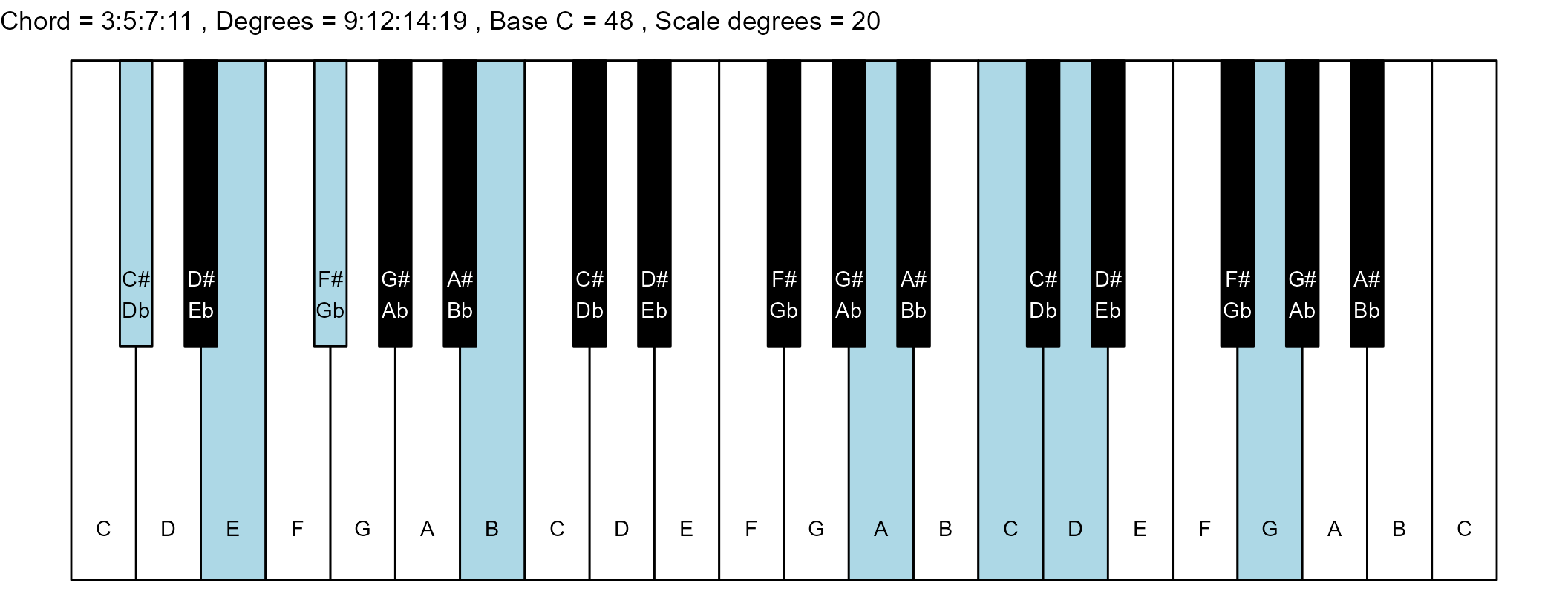
#> 23: 3:5:7:11 9:12:14:19 12 0
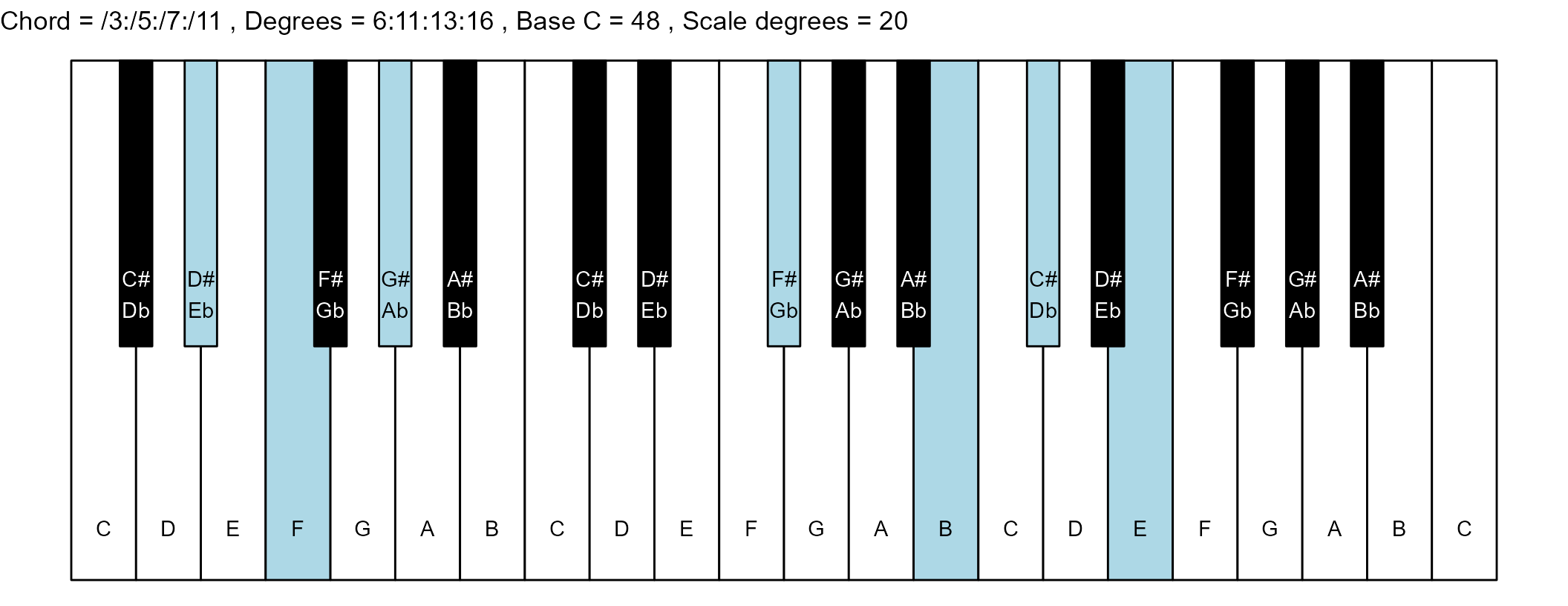
#> 24: /3:/5:/7:/11 6:11:13:16 12 1
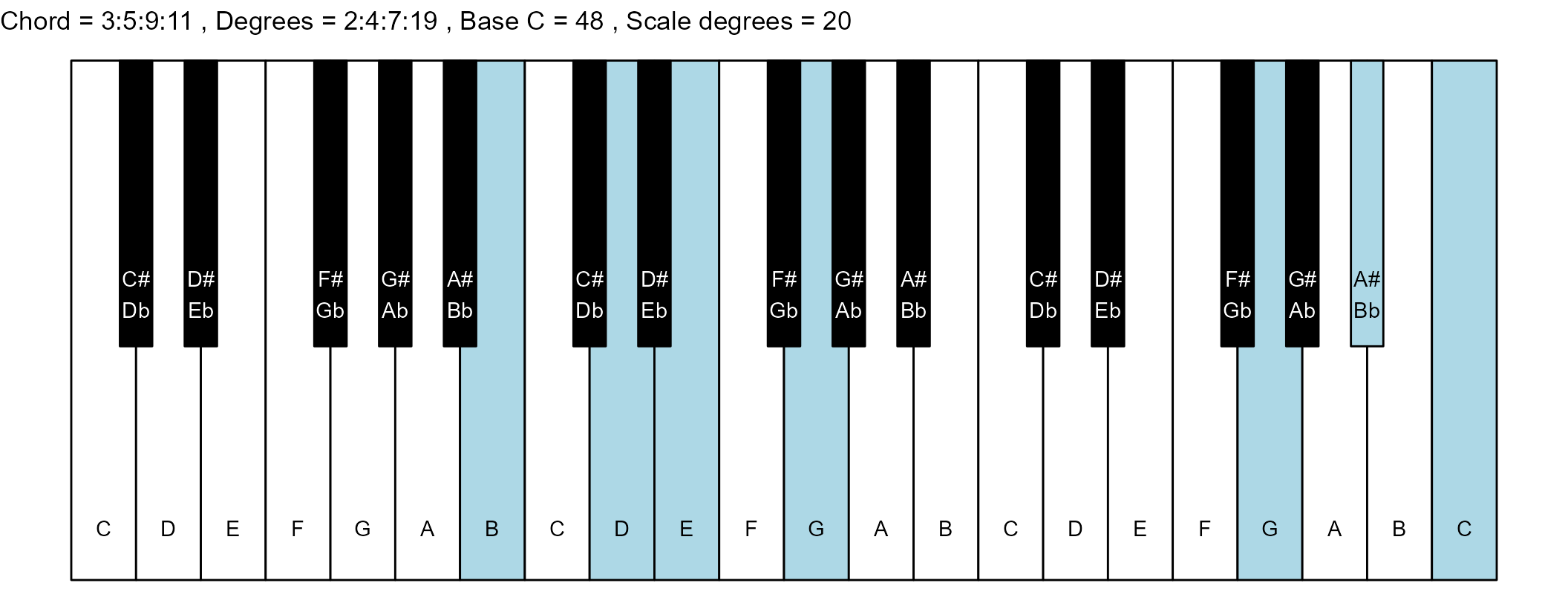
#> 25: 3:5:9:11 2:4:7:19 13 0
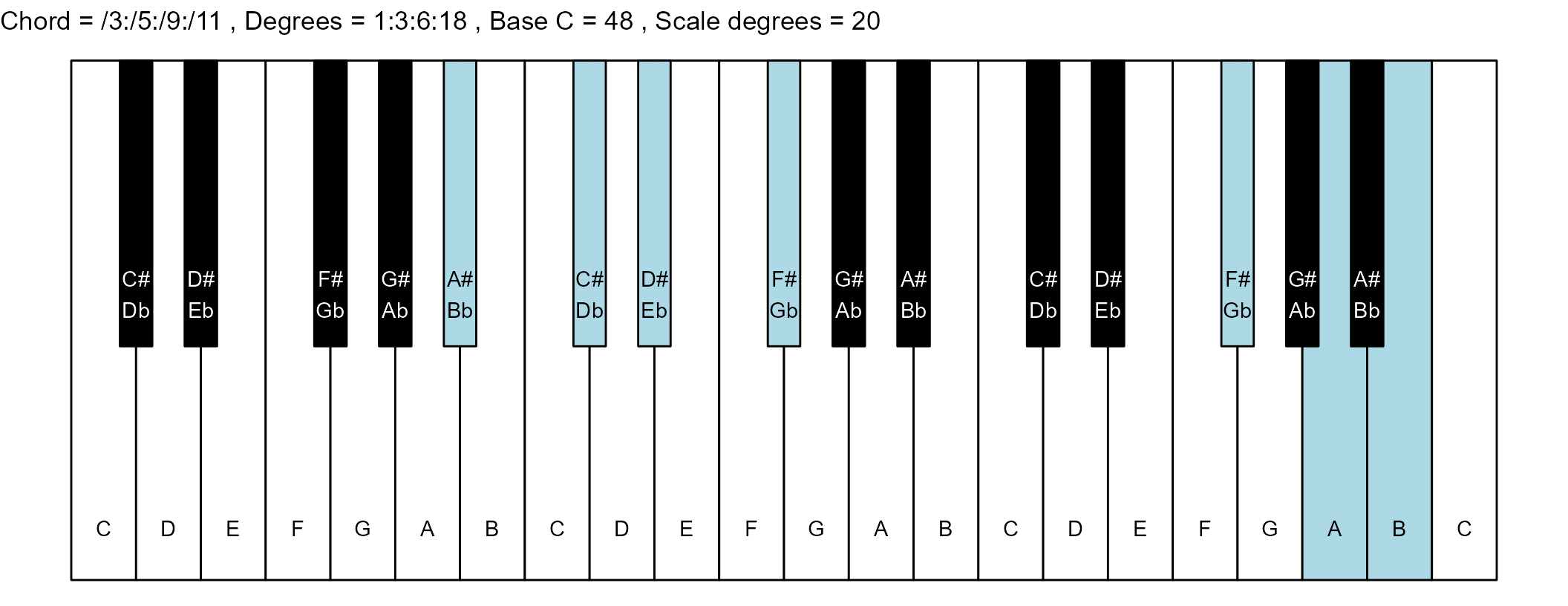
#> 26: /3:/5:/9:/11 1:3:6:18 13 1
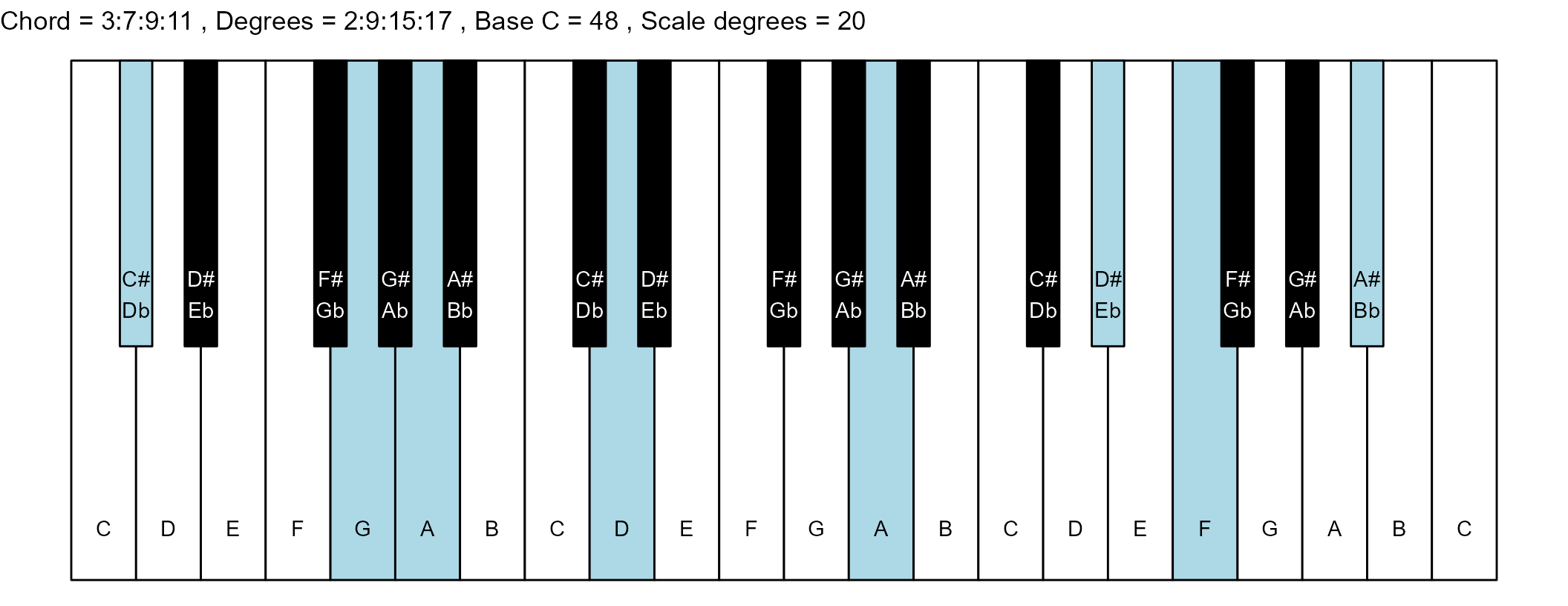
#> 27: 3:7:9:11 2:9:15:17 14 0
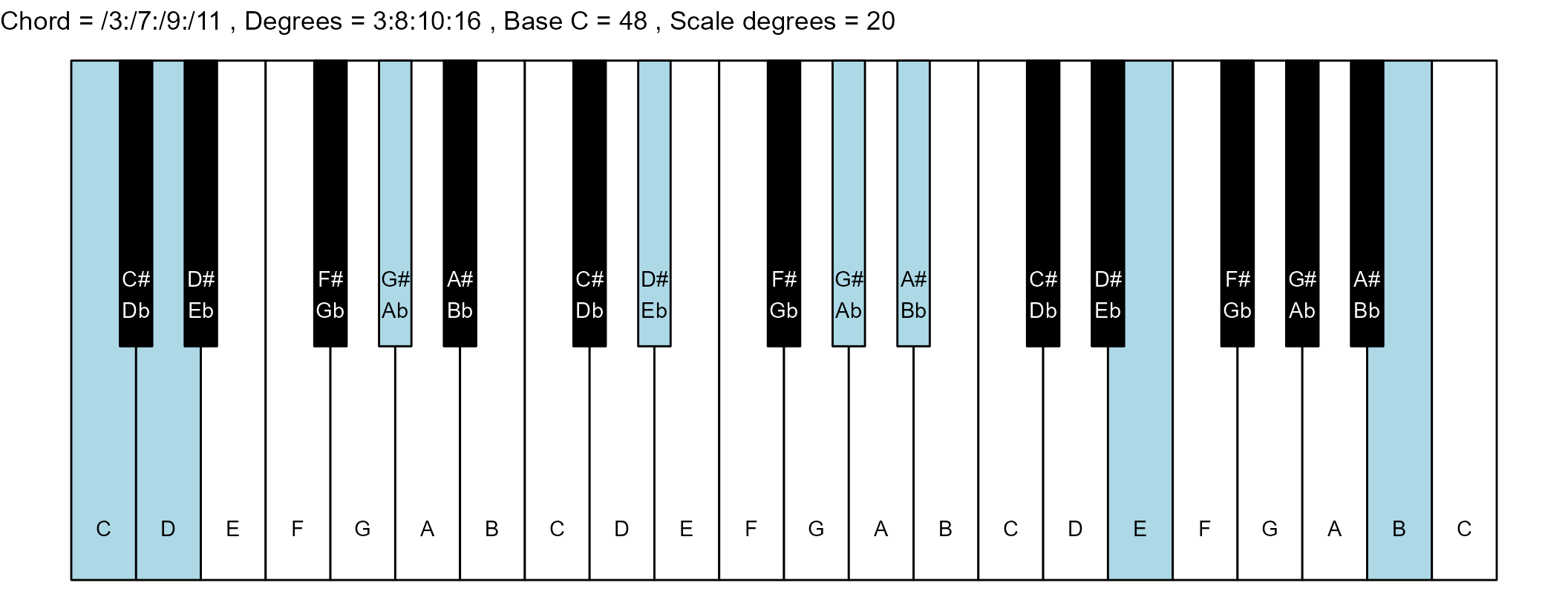
#> 28: /3:/7:/9:/11 3:8:10:16 14 1
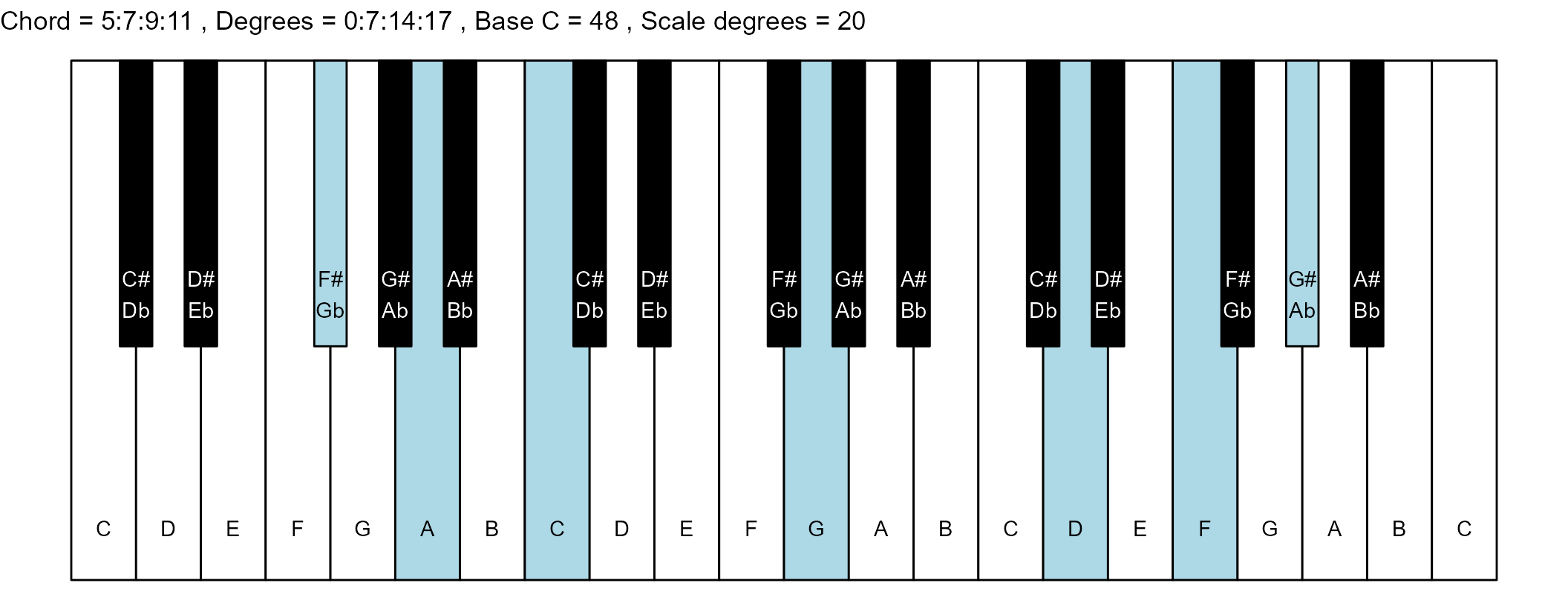
#> 29: 5:7:9:11 0:7:14:17 15 0
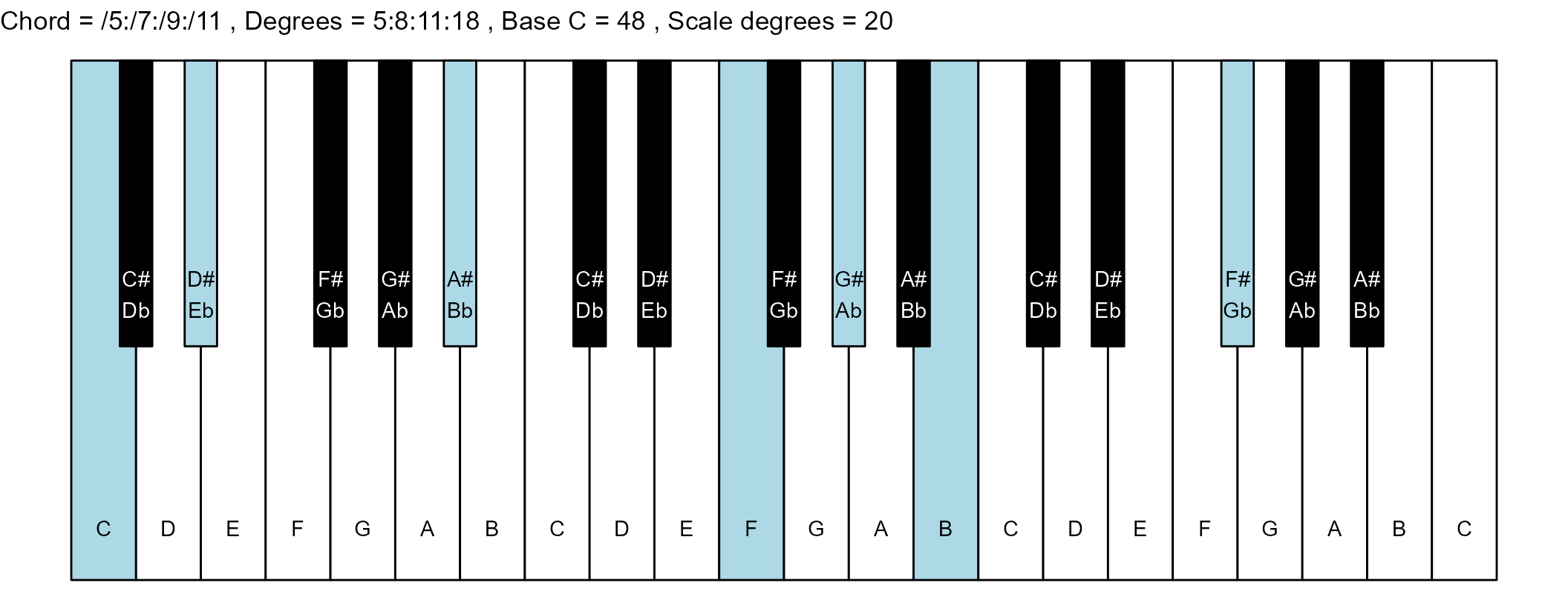
#> 30: /5:/7:/9:/11 5:8:11:18 15 1
#> chord degrees chord_index is_subharm
#> <char> <char> <int> <num>The plots
scale_degrees <- length(scale$degree) - 1
base_note_number = 48
chord_names <- chords$chord
degrees <- chords$degrees
degrees_matrix <- matrix(
unlist(lapply(strsplit(degrees, ":"), as.numeric)),
byrow = TRUE,
nrow = length(degrees)
)
for (ichord in 1:nrow(degrees_matrix)) {
chord_vector <- degrees_matrix[ichord, ]
title_string <- paste(
"Chord =",
chord_names[ichord],
", Degrees =",
degrees[ichord],
", Base C =",
base_note_number,
", Scale degrees =",
scale_degrees,
sep = " "
)
piano_plot <- chord_plot(
chord_vector, title_string, map, base_note_number
)
print(piano_plot)
}